

Imagine that we are trying to find the area of a lawn so that we can determine how much grass seed to purchase. The lawn is the green portion in Figure \(\PageIndex\).
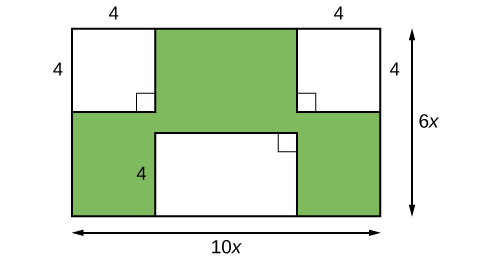
The area of the entire region can be found using the formula for the area of a rectangle.
The areas of the portions that do not require grass seed need to be subtracted from the area of the entire region. The two square regions each have an area of \(A =s^2=4^2= 16\; units^2\). The other rectangular region has one side of length \(10x−8\) and one side of length \(4\), giving an area of
\[A =lw=4(10x−8)=40x−32\; \text^2. \nonumber\]
So the region that must be subtracted has an area of
\[2(16)+40x−32= 40x\; \text^2. \nonumber\]
The area of the region that requires grass seed is found by subtracting \(60x^2−40x\; \text^2\). This area can also be expressed in factored form as \(20x (3x−2)\; \text^2\). We can confirm that this is an equivalent expression by multiplying.
Many polynomial expressions can be written in simpler forms by factoring. In this section, we will look at a variety of methods that can be used to factor polynomial expressions.
When we study fractions, we learn that the greatest common factor (GCF) of two numbers is the largest number that divides evenly into both numbers. For instance, \(4\) is the GCF of \(16\) and \(20\) because it is the largest number that divides evenly into both \(16\) and \(20\) The GCF of polynomials works the same way: \(4x\) is the GCF of \(16x\) and \(20x^2\) because it is the largest polynomial that divides evenly into both \(16x\) and \(20x^2\).
When factoring a polynomial expression, our first step should be to check for a GCF. Look for the GCF of the coefficients, and then look for the GCF of the variables.
The greatest common factor (GCF) of polynomials is the largest polynomial that divides evenly into the polynomials.
Factor \(6x^3y^3 +45x^2y^2+21xy\).
Solution
First, find the GCF of the expression. The GCF of \(6\), \(45\), and \(21\) is \(3\). The GCF of \(x^3\),\(x^2\), and \(x\) is \(x\). (Note that the GCF of a set of expressions in the form \(x^n\) will always be the exponent of lowest degree.) And the GCF of \(y^3\),\(y^2\), and \(y\) is \(y\). Combine these to find the GCF of the polynomial, \(3xy\).
Next, determine what the GCF needs to be multiplied by to obtain each term of the polynomial. We find that
Finally, write the factored expression as the product of the GCF and the sum of the terms we needed to multiply by.
Analysis
After factoring, we can check our work by multiplying. Use the distributive property to confirm that
Factor \(x(b^2−a)+6(b^2−a)\) by pulling out the GCF.
Although we should always begin by looking for a GCF, pulling out the GCF is not the only way that polynomial expressions can be factored. The polynomial \(x^2+5x+6\) has a GCF of \(1\), but it can be written as the product of the factors \((x+2)\) and \((x+3)\).
Trinomials of the form \(x^2+bx+c\) can be factored by finding two numbers with a product of \(c\) and a sum of \(b\). The trinomial \(x^2+10x+16\), for example, can be factored using the numbers \(2\) and \(8\) because the product of those numbers is \(16\) and their sum is \(10\). The trinomial can be rewritten as the product of \((x+2)\) and \((x+8)\).
A trinomial of the form \(x^2+bx+c\) can be written in factored form as \((x+p)(x+q)\) where \(pq=c\) and \(p+q=b\).
No. Some polynomials cannot be factored. These polynomials are said to be prime.
Solution
We have a trinomial with leading coefficient \(1\), \(b=2\), and \(c=−15\). We need to find two numbers with a product of \(−15\) and a sum of \(2\). In Table \(\PageIndex\), we list factors until we find a pair with the desired sum.
| Factors of −15 | Sum of Factors |
|---|---|
| 1,−15 | −14 |
| −1,15 | 14 |
| 3,−5 | −2 |
| −3,5 |
Now that we have identified \(p\) and \(q\) as \(−3\) and \(5\), write the factored form as \((x−3)(x+5)\).
Analysis
We can check our work by multiplying. Use FOIL to confirm that \((x−3)(x+5)=x^2+2x−15\).
No. Multiplication is commutative, so the order of the factors does not matter.
Trinomials with leading coefficients other than \(1\) are slightly more complicated to factor. For these trinomials, we can factor by grouping by dividing the x term into the sum of two terms, factoring each portion of the expression separately, and then factoring out the GCF of the entire expression. The trinomial \(2x^2+5x+3\) can be rewritten as \((2x+3)(x+1)\) using this process. We begin by rewriting the original expression as \(2x^2+2x+3x+3\) and then factor each portion of the expression to obtain \(2x(x+1)+3(x+1)\). We then pull out the GCF of \((x+1)\) to find the factored expression.
To factor a trinomial in the form \(ax^2+bx+c\) by grouping, we find two numbers with a product of \(ac\) and a sum of \(b\). We use these numbers to divide the \(x\) term into the sum of two terms and factor each portion of the expression separately, then factor out the GCF of the entire expression.
Factor \(5x^2+7x−6\) by grouping.
Solution
We have a trinomial with \(a=5\),\(b=7\), and \(c=−6\). First, determine \(ac=−30\). We need to find two numbers with a product of \(−30\) and a sum of \(7\). In the table below, we list factors until we find a pair with the desired sum.
| Factors of −30 | Sum of Factors |
|---|---|
| 1,−30 | −29 |
| −1,30 | 29 |
| 2,−15 | −13 |
| −2,15 | 13 |
| 3,−10 | −7 |
| −3,10 | 7 |
\(5x^2−3x+10x−6\) Rewrite the original expression as \(ax^2+px+qx+c\).
\(x(5x−3)+2(5x−3)\) Factor out the GCF of each part
\((5x−3)(x+2)\) Factor out the GCF of the expression.
Analysis
We can check our work by multiplying. Use FOIL to confirm that \((5x−3)(x+2)=5x^2+7x−6\).